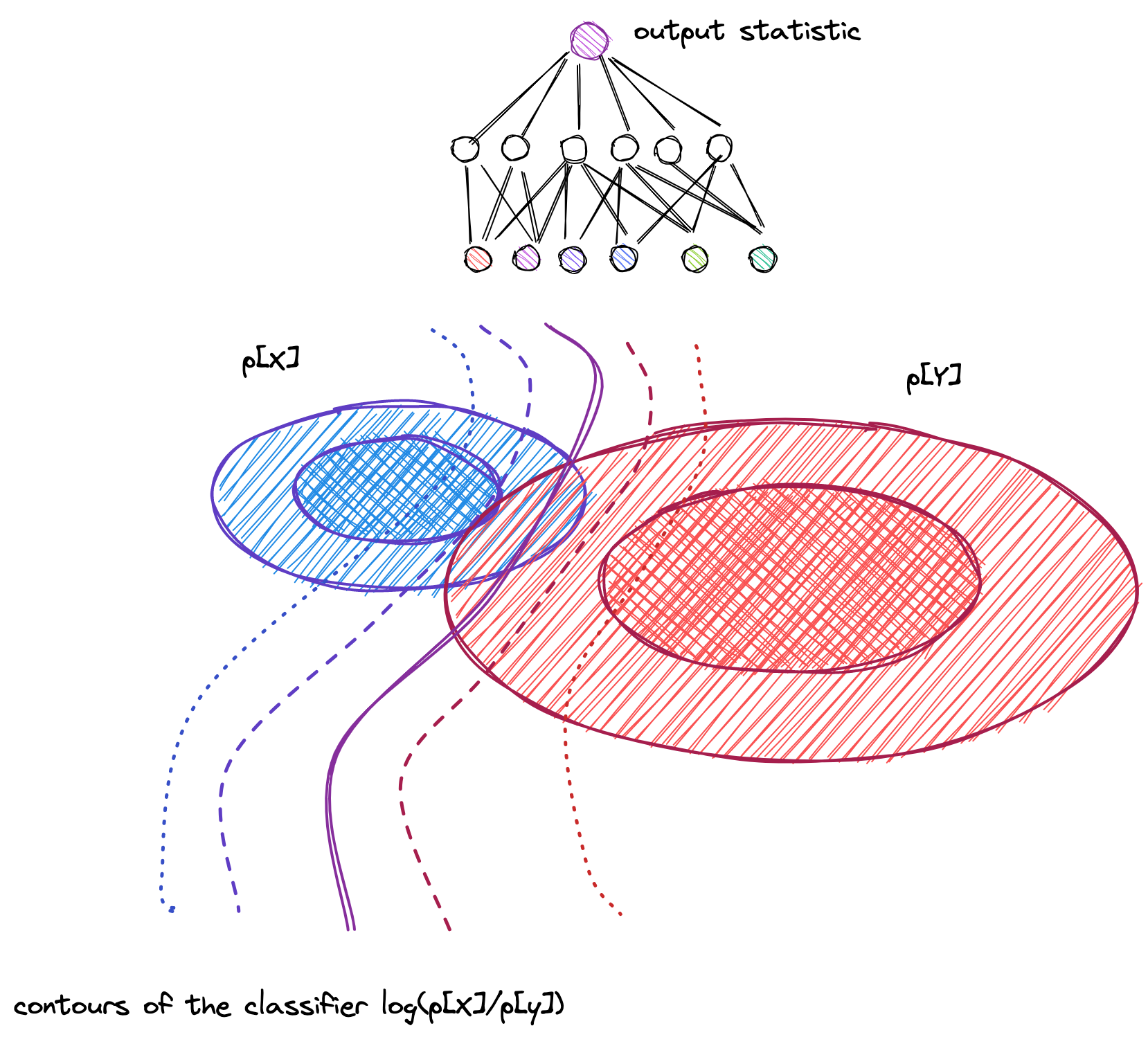
Classifiers for Likelihoods: Why Logistic?
If you train a binary classifier to minimize the logistic-loss in distinguishing two datasets $X$ and $Y$, then, as if by magic, your classifier statistic is an approximation for the likelihood ratio of the two distributions $p_X/p_Y$. What black magic is this?
When I tried to understand likelihood free inference, I found the literature tended to focus on the Neyman-pearson lemma as the link between classifiers and probabilities. The Neyman-pearson lemma is a statement that the best classification statistic you can get is the likelihood. Therefore it follows in the reversal of this logic, that if you have trained an optimal classifier, you've also, (perhaps unwittingly!) performed likelihood approximation.
The key point here being "roughly speaking". The Neyman-Pearson lemma, is a kind of asymptotic and technical result, and it is not at all clear to me how to use it to extract a probability from a classifier.
The link between classifiers and likelihoods couldn't be simpler and the Neyman-Pearson lemma is not really a part of the story: The logistic-loss functions that we train the classifier will converge in the large data limit to the cross entropy. The cross entropy is minimized by the true class probability. Therefore, when your classifier minimizes the loss, it must return the true class probability. The magic of likelihood free inference is no magic at all: When you used the logistic loss function, you were asking for the true probability (if possible) as your class statistic!
Or in another sense, there is magic, but the magic isn't in the classification, it is in the loss function. The logistic loss-function is special. Other standard loss functions, such as 0-1 loss are not that special, and you won't get likelihoods out. But just how special is the logistic loss?
When is classifier output probabilistically meaningful?
Suppose you have an estimator for the class probabilities $\hat{p}_c$. The cross-entropy (=logistic) loss-function has this amazing property that allows you to assymptotically reconstruct the true probabilities from your classifier outputs if your classifer is rich enough. This property arises from the facts that
1.) The cross-entropy of the class probability is minimized by the true distribution, i.e.
\begin{equation} \arg \min_{\hat{p}_c} H(p_c||\hat{p}_c) = p_c \end{equation}
2.) The minimizer of the positive weighted sum of independent functions is the minimizers of independent functions.
\begin{equation} \arg \min_{\hat{p}_c(x)} \sum_x p(x) H(p_c(x)||\hat{p}_c(x)) = p_c(x) \end{equation}
Tricky! Note this "if your classifer is rich enough" caveat: if your classifier is not rich enough, it may not be able to fully represent the vector function $p_c(x)$.
In what sense is the cross-entropy loss unique in this way? The cross entropy is far from being the only notion of "distance" on probability distributions, many other functiosn have the property that $ \arg \min_{\hat{p}} D(p||\hat{p}) = p $. Notable there are the rich families of Renyi divergences which have many lovely properties. The cross-entropy can be viewed as an offset version of the most famous Renyi divergence of all, the KL divergence $$ H(p||\hat{p}) = D_{KL}(p||\hat{p}) +S(p) $$
But the cross entropy is quite a special Renyi divergence in this sense. The decomposition means that we have a divergence which can be written purely as the expectation of a function which only depends on the probability estimator $\hat{p}$, and not on the true distribution $\hat{p}$.
$$ L(p,\hat{p}) = \underset{c\sim p}{E} \log \hat{p}_c. $$
This means we can use the empirical estimator of this function as the loss function for optimising a neural net. It's easy to check that no other Renyi-divergence can be written this way, with the $p$-dependence entirely in the expectation (up to an additive constant). Is the cross entropy perhaps unique? That is, are there other functions $f$ such that $ \arg \min_{\hat{p}} \underset{c\sim p}{E} f_c(\hat{p}) = p ? $
If there are, they have empirical loss functions that are in some sense "equally good". $$ l(X) = \sum_{i} f_{c^{(i)}}(\hat{p}(x^i)) $$ Equally good in that, given enough data, and a rich enough clsssifier, you get the likelihood out.
The answer, which was worked out by Savage, is that the cross entropy is actually one of many such interesting functions. We follow this neurips 2008 paper, but extend it slightly to the general $k$-ary classifier case.
The derivation is straightforward, but it took people a long time to work out properly. I think part of the reason this problem was hard is because of a tempting and false argument which I've stumbled over multiple times.
An incorrect argument for the uniqueness of the cross entropy.
Here's the wrong argument, and notice the subtle notational change in the way $f_c(\hat{p})$ is written as $f(\hat{p}_c)$.
Suppose we minimize $L$ subject to the normalization condition with a lagrange multiplier at $\hat{p}_c = p_c$, This leads to the vector equation
$$ p_c f'(p_c) = λ, \, ∀c $$
Looks cut and dried: $f'(p_c) = λ/p_c $, $f(p_c) = λ \log p_c$. It's just the cross-entropy and only the cross-entropy (up to a multiplicative factor at least) seems to come out of this argument.
What makes the argument wrong is that the functions $f_c(\hat{p})$ are allowed to be much richer than simple functions $f(\hat{p}_c)$. Each $f_c$ can depend on the whole probability vector $\hat{p}_{c'}$. Thus, each $f_c$ is, in general a function on a high-dimensional vector space with dimension equal to the number of classes $k$.
The general requirements for "probability elicitation"
Understanding $∂_{p_{c'}} f_{c}(p)$ as a gradient of a function on the full probability vector, gives a set of minimization equations $$ λ = \sum_c p_c ∂_{p_{c'}} f_c(p) \, \forall c' $$ Define the minimum value as a function of the true distribtuion $Q(p) = \sum_c p_c f_c(p)$. In the cross-entropy setting $Q$ is just the self entropy $Q(p) = \sum_c p_c \log p_c$. As with the self-entropy, Q must be strictly convex so that the minimum of $D_f(p,\hat{p})$ is unique.
Our goal will be to write everything in terms of $Q$ and its gradients $∂_{p_{c}} Q(p) = f_c(p) + λ$. Taking the average over $p_c$ and using the normailzation condition to craft a scalar equation for $λ$, $$ λ = \sum_c p_c ∂_{p_{c}} Q(p) - Q(p) $$ This is how these lagrange mulitplier equations go, you use your constraint to get equation for your λ's. This yields $$ ∂_{p_{c}} Q(p) - \sum_{c'} p_{c'} ∂_{p_{c'}} Q(p) + Q(p) = f_c(p) $$
So for any differentiable function of $|C|$ variables, which we call $Q(p)$, which is convex in terms of $p$, there exists a loss function can be used to get a probability estimate in a supervised learning context.
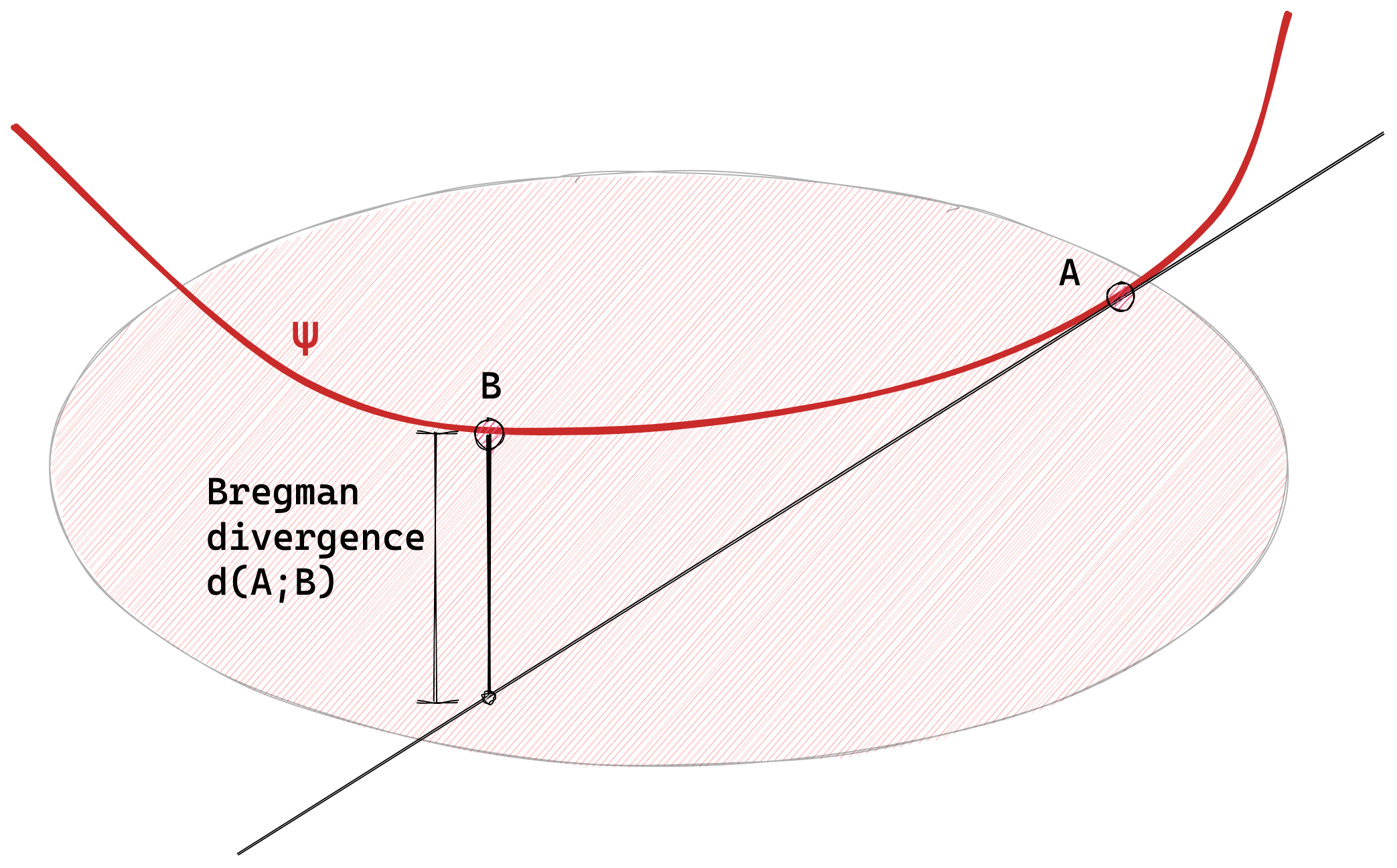
Bregman divergences
The fact that a convex function generates a loss function on probability space makes this look a lot like Bregman divergence, which are also divergences determined by some choice of convex function. Indeed if we ensure that our loss function has a minimum of zero, by subtracting off $Q(p)$, we see that the loss function is indeed a Bregman divergence generated by $Q$,
$$ \sum_{c} p_c f_c(\hat{p}) - Q(p) = \left( p - \hat{p} \right) · ∂_{\hat{p}} Q(\hat{p}) + Q(\hat{p}) - Q(p) = d_Q(\hat{p}, p) $$ The empirical loss function is then just the linear part of $d_Q(\hat{p}, p)$, the part that doesn't depend on $p$. The cross entropy $Q$ is $$ Q(p) = \sum_c p_c \log p_c $$
So in conclusion we can summarize this train of thought with: probabilistically meaningful classifiers are trained with a Bregman type loss function expressed on the vector space $p_c$, the class probabilities.
It is quite amazing to me that though classifers go back to the 70's it is not really until the 2010's that this really basic statistical fact appears to be well known.
Note, coordinate transformations of a Bregmann divergence are not again Begmann divergences, so there really is a priviledged vector space here: the class probabilities $p_c$. This is kind of surprising, the vector space in information geometry is usually the $log$-probabilities (see Shun-ichi Amari's wonderful book for a deep study of nautral parameters and statistical manifolds). But the algorithmic important of this Bregmann form for likelihood-free inference make me think that this class of Bregmann Divergences on non-logged prababilities is at least as important as that on natural parameters.
What's cool is how easily you can derive the Bregman form from a constructive, engineering perspective. The Bregman form isn't some abstract weirdo distance function (well, okay... yes it is). It has non-trivial algorithmic meaning and it is useful for performing probabilistic calculations with a computer.